Case Study of Statistics in the Fracture of Laminated Composites


Influence of Ply Cracks on Fracture Strength of Graphite/Epoxy Laminates at 76 K

Introduction

The objective of this case study is to show how the statistical analysis of a data set must be interpreted in context with other information if meaningful conclusions are to be made by the materials researcher. Here we show that when combined with a fractographic investigation and stress analysis, results of a statistical analysis is not only more meaningful but for the materials researcher point of view such an approach can be used to verify the existence of a statistical "weak-link" effect. The objective here is to study and explain what is meant by the "weak-link" effect.

Below a visual summary is given, that is complete, but intentionally left without much explanation so that the student reading this case study can come to independent conclusions and perhaps conclusions that are different from the original researcher.

The original raw data sets are provided via hyperlinks in the figure captions were students can down load these data sets and perform an independent statistical analysis as part of their effort to explain how composite laminates fracture.

Experimental Procedure

A total of 73 [0/+45/-45/90]s, 73 [0/90/+45/-45]s, and 70 [08] specimens were fabricated from the same batch of graphite epoxy. All specimens were 10.2 cm long with uniform width. Quasi-isotropic laminates were 1.27 cm wide and and unidirectional specimens were 0.64 cm wide. Half of the specimens of each type were exposed to 95% relative humidity at 338 K until no additional absobed moisture wight gain could be measured (WET or saturated condition). The remaining specimens were dried in an oven at 338 K until no additional moisture wight loss could be measured (DRY or dehydrated condition). Thirty-five WET and 35 DRY quasi-isotropic laminates were quasi-statically loaded in tension to fracture using a hydraulic load controlled system. A special cryogenic load fixture and extensometer , 1.27 cm gage length, were designed to load specimens in tension with causing additional loads due to thermal contraction at 76 K, Ref [2]. All specimens had glass epoxy tabs to minimize stress concentrations. All specimens were loaded in increments of 445 N, and edge replicas of damage were recorded onto acetate strips. Hence, the load increment resulting in the intiating ply cracks was recorded. All specimens were loaded to failure. All failed specimens from the four populations:

were posted for postmortem fractorgraphic and statistical analysis and shown here in the figures below. We have also segregated specimens from the WET:[08] into four groups: From these four groups are the fracture strengths representative of the same population or are the four groups statistical different as their fracture surfaces would indicate.

Explanation of Visual Summary Below

Below a visual summary is given, that is complete, but intentionally left without much explanation so that the student reading this case study can come to independent conclusions and perhaps conclusions that are different from the original researcher. A brief explanation is provided above for the various composite laminate types, intent of this research, a description of the experimental procedure, and references which provide the details of this research.

These figures will also be referenced in the class lectures. Please note that raw data sets associated with some of the figures can be downloaded via hyperlinks in the figure captions.


Figure 1. Edge acetate replica showing a Ply Crack and individual 0 degree fiber failures in the load bearing ply of a Type II: [0/90/+45/-45]sLaminate


Figure 2. Comparison of representative WET and DRY fractures of [0/90/+45/-45]s


Figure 3. Comparison of entire population of WET (IIWET.DAT) and DRY (IIDRY.DAT) fractures of Type II: [0/90/+45/-45]s Laminates


Figure 4. Comparison of entire population of WET (IWET.DAT) and DRY (IDRY.DAT) fractures of Type I: [0/+45/-45/90]s Laminates


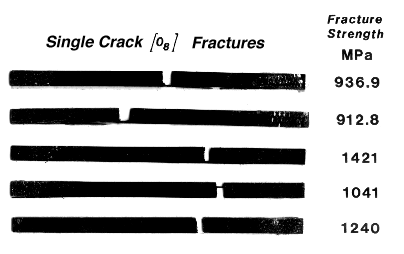
Figure 5a. Selected [08] (O8DOM.DAT) fracture surfaces that were unusually clean


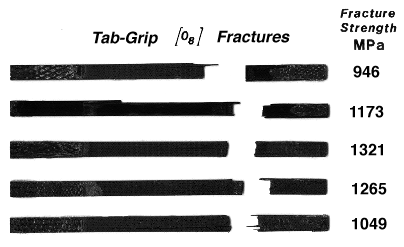
Figure 5b. Selected [08] (O8GRIP.DAT) fracture surfaces at or near grip


Figure 5c. Selected [08] (O8STAG.DAT) fracture surfaces that were staggered


Figure 5d. Selected [08] (O8BROM.DAT) fracture surfaces that were "broomed" (most common)

SEM Fractography

Scanning electron microscope (SEM) fractographs of fracture surfaces representative from each population is shown below for a Type II: [0/90/+45/-45]s only.

(a)
(b)
(c)

(d)
(e)
Figures 6 a), b), c), d), e). Fracture surfaces of WET [0/90/+45/-45]s laminates

.

(a)
(b)
(c)

(d)
(e)
Figures 7 a), b), c), d), e). Fracture surfaces of DRY [0/90/+45/-45]s laminates

.

Stress Analysis

Details of the stress analysis is given in Reference [2]. Here we a schematic of the laminate and finite element mesh that was used to model a ply crack in a [0/90/+45/-45]s laminate and the stress gradients ("concentrations") in the load bearing 0 degree ply near the ply crack tip.


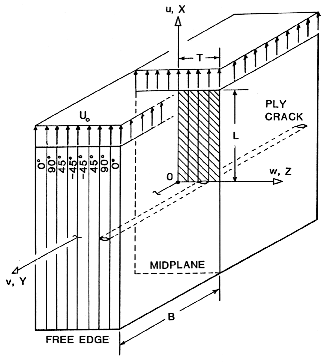
Figure 7. Schematic of Ply Crack in a [0/90/+45/-45]s laminate


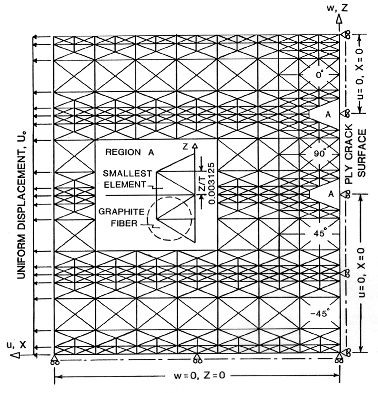
Figure 8. Ply crack finite element grid at laminate midplane.


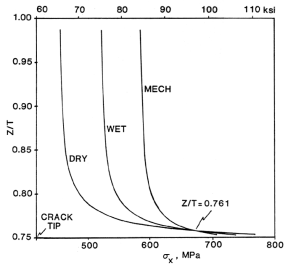
Figure 9. Mode I stress in the x-direction in the 0 degree load bearing ply above a Ply Crack.


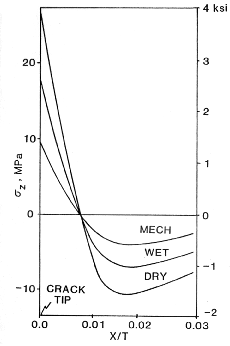
Figure 10. Mode I interface stress in the z-direction between the 0 degree and 90 degree plies next to the Ply Crack.


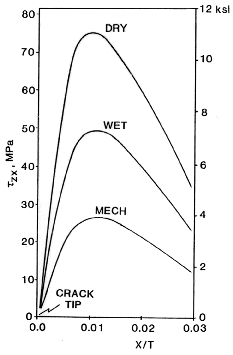
Figure 11. Mode II interface shear stress along the interface of the 0 degree and 90 degree plies next to the Ply Crack.

Statistical Results


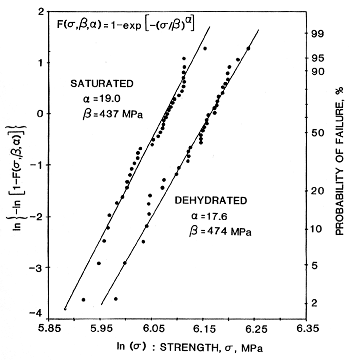
Figure 12. Weibull plot of WET and DRY [0/90/+45/-45]s strengths.

Analytic Models of Continuous Damage Mechanics (CDM)


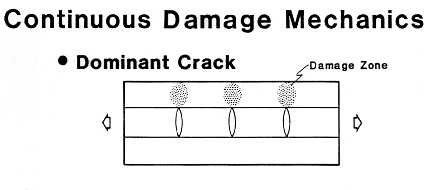
Figure 13. Formation of damage zones in 0 degree load bearing ply near Ply Crack


Figure 14. Edge acetate replica showing Ply Cracks and 0 degree fiber fracture damage zones


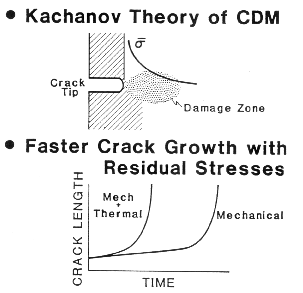
Figure 15. Kachanov Theory of CDM predicting faster crack growth when residual thermal stress are present
Last Revised November 2020
http://www.sv.rkriz.net/class/surp/surp96/laughlin/stat/MatlExample/MatlExample.html